Specialist Mathematics UDFs
Calculus
Arc Length (arclength)
Function: Determines the arc length for parametric curve
Case 1: Function
Syntax: arclength(Function, Variable, Lower Bound, Upper Bound)
Example:
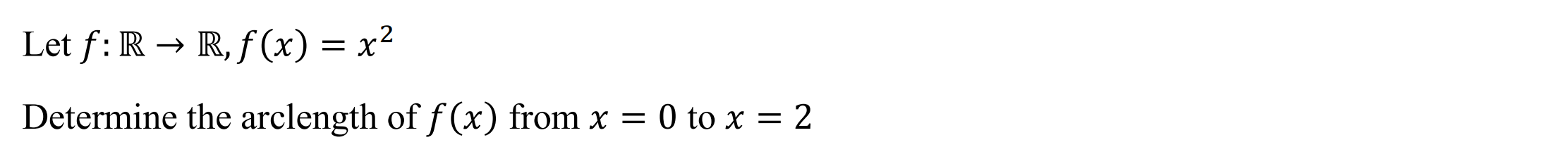

Case 2: Parametric Equation
Syntax: arclength(Vector, Variable, Lower, Upper)
Example:
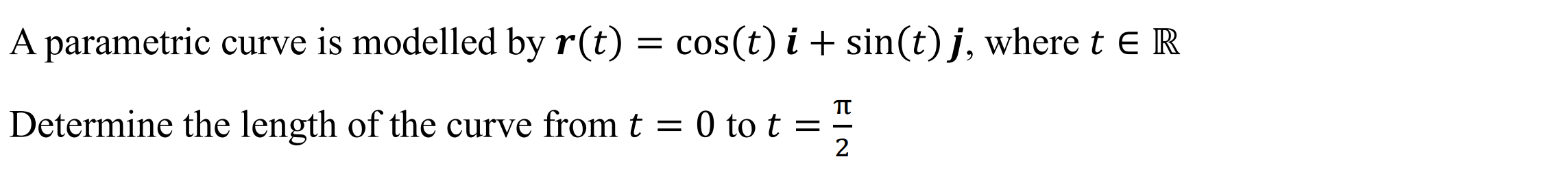

Bound Volume (boundvol)
Function: Determines the volume of the solid formed by the region(s) bound by two curves
Syntax: boundvol(Function 1, Function 2, Variable)
Example:


Bound Volume Domain (boundvold)
Function: Determines the volume of the solid formed by the region(s) bound by two curves in a restricted domain
Syntax: boundvold(Function 1, Function 2, Variable, Lower Bound, Upper Bound)
Example:
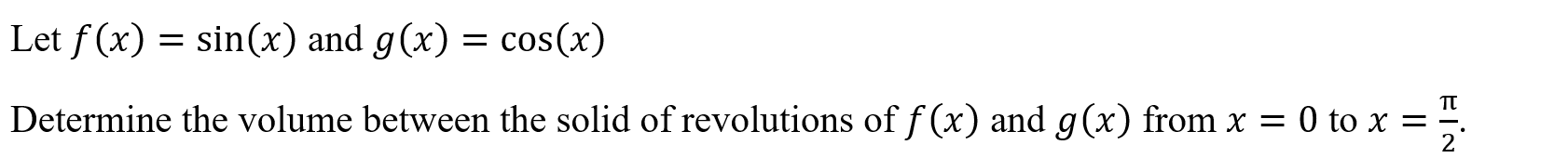

Euler's Method (eulers)
Function: Uses euler's method to estimate the solution to a differential equation
Syntax: eulers(Differential Equation, Independent Variable, x0, xn, y0, step-size)
Example:
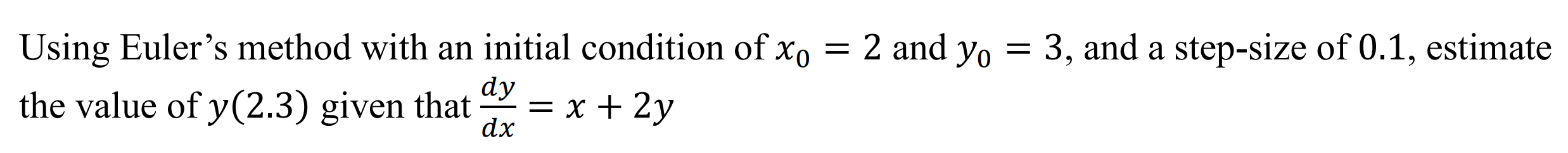

Mixing Problems (mix)
Function: Determines the differential equation of the mixing problem
Syntax: mix() (You will be prompted for inputs)
Example:


Rational Function (rational)
Function: Determines holes, straight line asymptotes, and oblique asymptotes of a rational function.
Syntax: rational(numerator, denominator, variable)
Example:
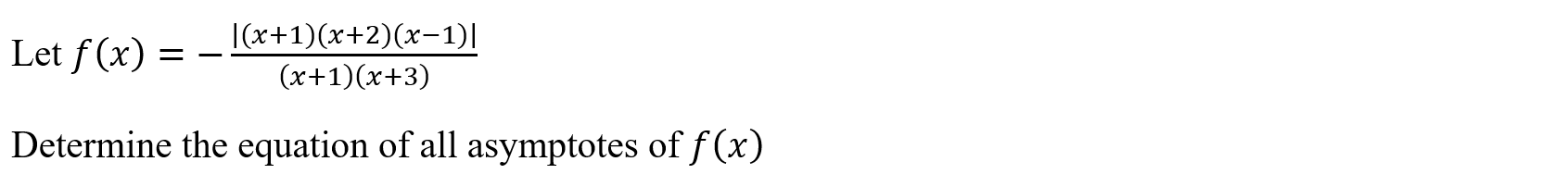

Surface Area of Solid (surfarea)
Function: Determines the surface area of a solid of revolution
Case 1: Function of x rotated about x-axis
Syntax: surfarea(Function, Variable, Lower Bound, Upper Bound)
Example:


Case 2: Function of y rotated about y-axis
Syntax: surfarea(Function, Variable, Lower Bound, Upper Bound)
Example:


Case 3: Function of x rotated about y-axis
Syntax: surfarea(Function, y, x-lower, x-upper)
Example:
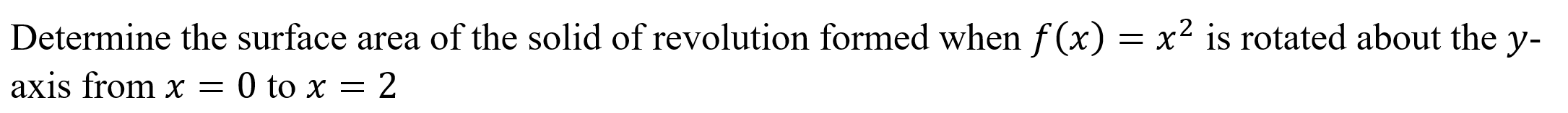

Case 4: Parametric Equation
Syntax: surfarea(Function, t, Lower Bound, Upper Bound)
Example:
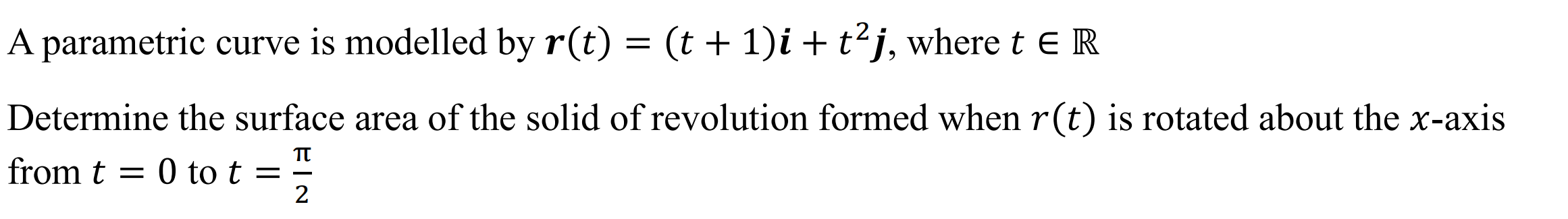

Complex Numbers
De Moivre's Theorem (demoiv)
Function: Determines the solutions to roots of unity questions
Syntax: demoiv(Power , Number)
Example:
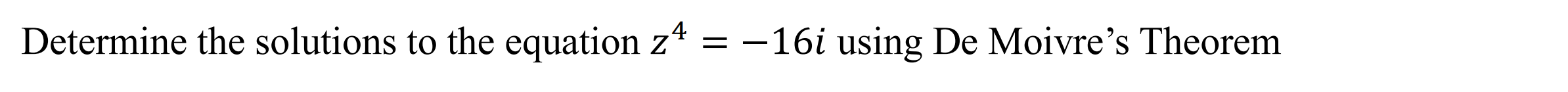

Circle Locus First Form (locicir1)
Function: Determines cartesian equation of circle loci in the form |z - a| = r
Syntax: locicir1(Point , Radius)
Example:


Circle Locus Second Form (locicir2)
Function: Determines cartesian equation of circle loci in the form |z - a| = k|z - b|
Syntax: locicir2(Point 1, Point 2, k)
Example:


Ellipse Locus (lociellp)
Function: Determines cartesian equation of ellipse loci
Syntax: lociellp(Point 1, Point 2, Length)
Example:
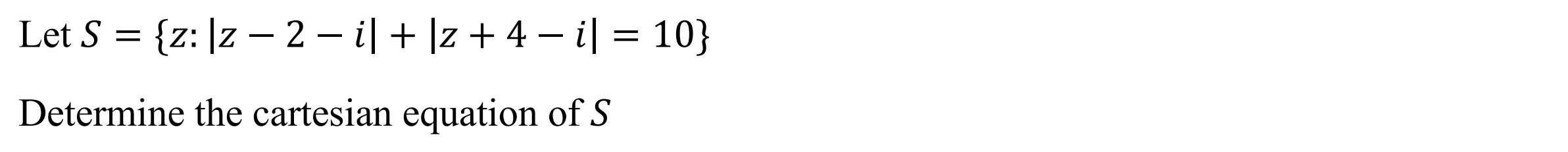

Hyperbola Locus (locihyp)
Function: Determines cartesian equation of hyperbola loci
Syntax: locihyp(Point 1, Point 2, Length)
Example:
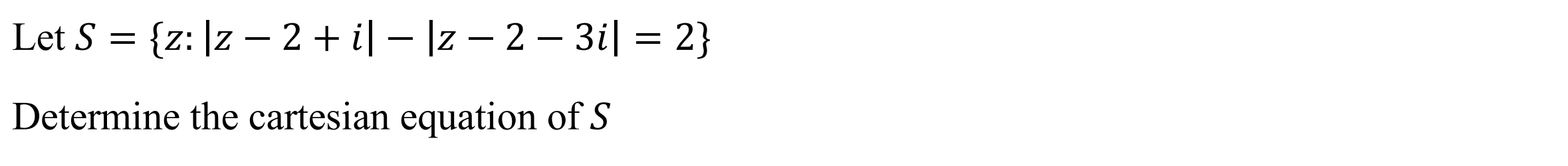

Line Locus (lociline)
Function: Determines cartesian equation of line in the form |z - a| = |z - b|
Syntax: lociline(Point 1, Point 2)
Example:


Quadratic Roots (quadroots)
Function: Determines quadratic roots of a complex number algebraically
Syntax: quadroots(Number)
Example:
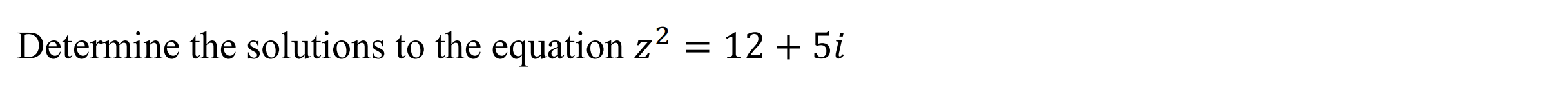

Ray (ray)
Function: Determines the cartesian equation of a ray given a point and an angle
Syntax: ray(Point, Angle)
Example:
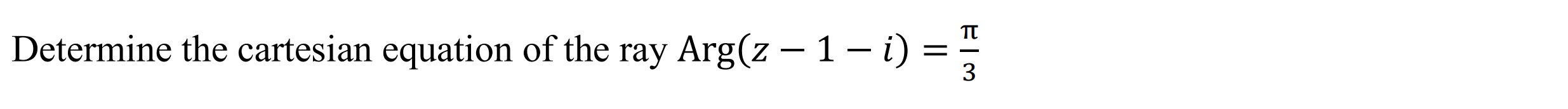

Kinematics
Collision Detector (collision)
Function: Determines whether two particles collide and where their paths intersect
Syntax: collision(Position Vector 1, Position Vector 2)
Example:


Projectile Motion (projm)
Function: Determines the accleration, velocity, position, max height, max displacement, return speed of a particle
Syntax: projm(Initial Position, Initial Velocity, Launch Angle, Initial Acceleration)
Example:


Constant Acceleration Equations (suvat)
Function: Enter 3 known values and 2 unknown variables, it will determine the unknowns
Syntax: suvat(s (displacement), u (initial velocity), v (final velocity), a (acceleration), t (time))
Example:


Vectors
Unit Vector Bisector (bisec)
Function: Determines the unit vector which bisects the angle between two vectors
Syntax: bisec(vector 1, vector 2)
Example:
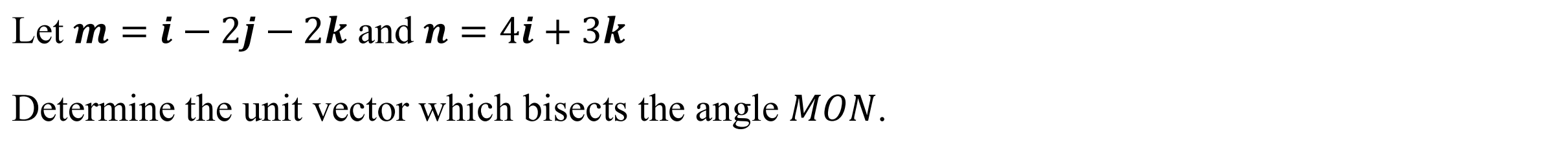

Colinear (colin)
Function: Determines value(s) of a variable required for points to be collinear
Syntax: colin(Point 1, Point 2, Point 3)
Example:
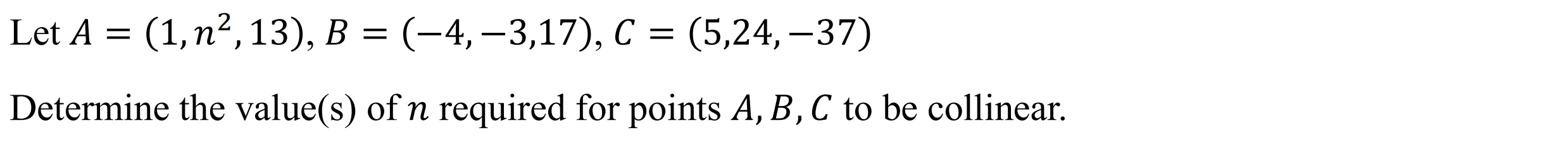

Linear Dependence (lindep)
Function: Determines value(s) of a variable required for 3 vectors to be linearly dependent
Syntax: lindep(Vector 1, Vector 2, Vector 3)
Example:
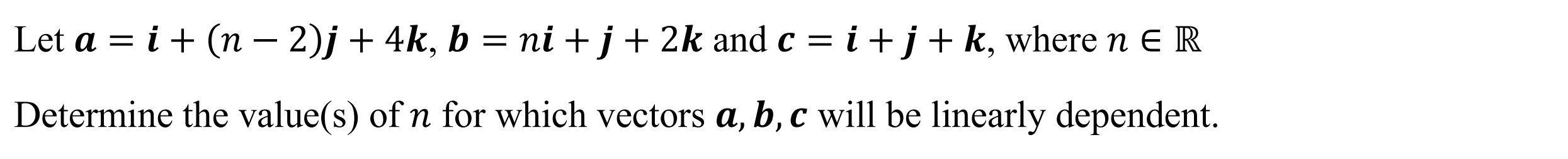

Angle between Vectors (vecang)
Function: Determines the angle between the two inputted vectors.
Syntax: vecang(Vector1, Vector2)
Example:


Vector Projection (vproj)
Function: Determines vector, scalar resolute, & angle for two inputted vectors
Syntax: vproj(Vector 1, Vector 2)
Example:


Linear Algebra
Line Cartesian to Vector (car2vecline)
Function: Converts equation of line from cartesian form to vector form
Syntax: car2vecline(line Cartesian)
Example:
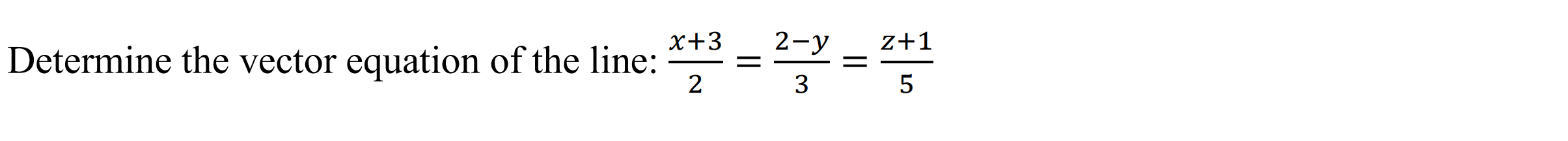

Plane Cartesian to Vector (car2vecplane)
Function: Converts equation of plane from cartesian form to vector form
Syntax: car2vecplane(Plane Cartesian)
Example:
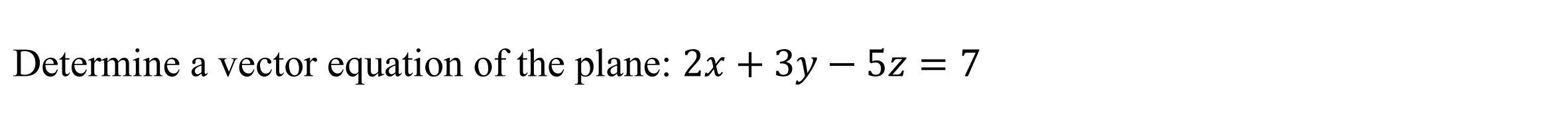

Line Vector to Cartesian (vec2carline)
Function: Converts equation of line from vector form to cartesian form
Syntax: vec2carline(line Vector)
Example:
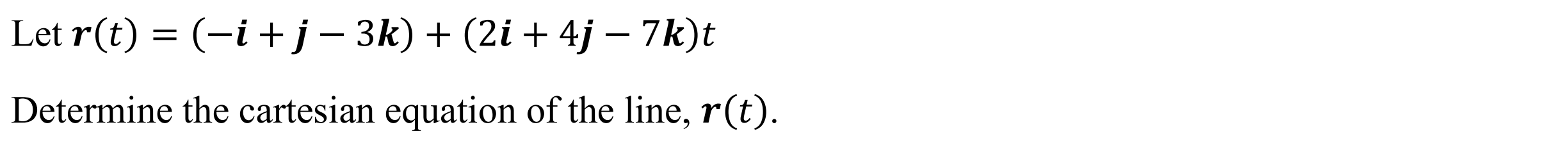

Plane Vector to Cartesian (vec2carplane)
Function: Converts equation of plane from vector form to cartesian form
Syntax: vec2carplane(Plane Vector)
Example:
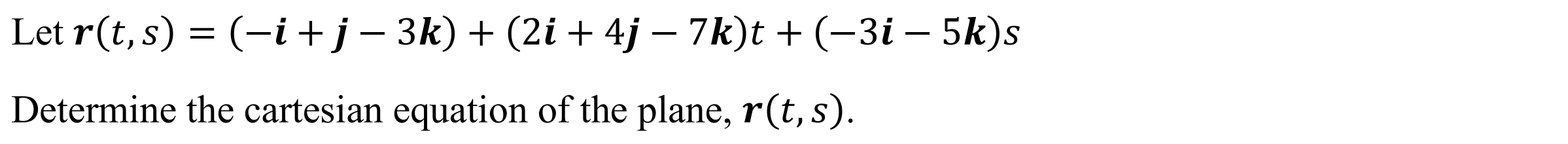

Minimum Distance between 2 lines (dist2l)
Function: Determines minimum distance between two lines
Syntax: dist2l(Line Vector 1, Line Vector 2)
Example:
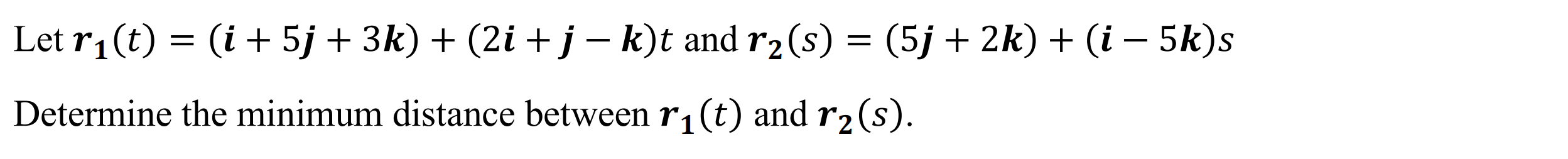

Minimum Distance between 2 planes (dist2pl)
Function: Determines minimum distance between two planes
Syntax: dist2pl(Plane Cartesian 1, Plane Cartesian 2)
Example:
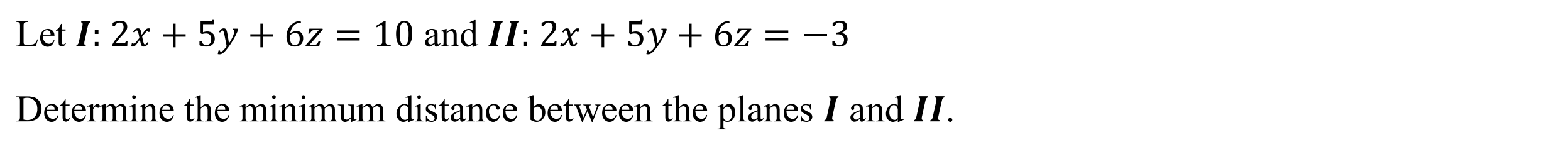

Minimum Distance between line and plane (distlpl)
Function: Determines the minimum distance between a plane and line
Syntax: distlpl(Line Vector, Plane Cartesian)
Example:
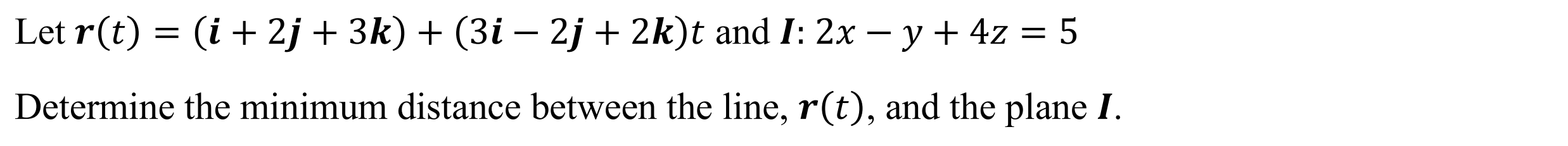

Minimum Distance between line and point (distlp)
Function: Determines minimum distance between a line and point
Syntax: distlp(Line Vector, Point)
Example:
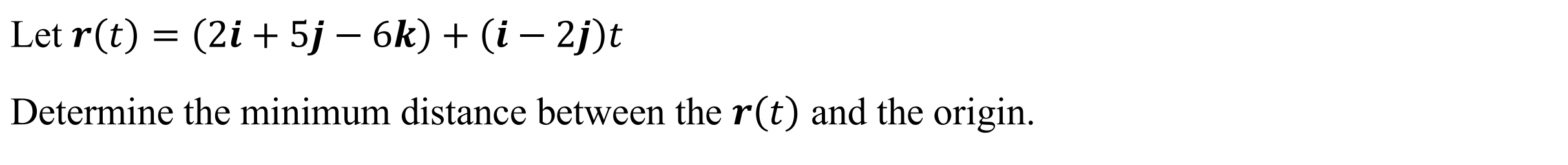

Minimum Distance between plane and point (distplp)
Function: Determines minimum distance between a plane and point
Syntax: distlp(Plane Equation, Point)
Example:
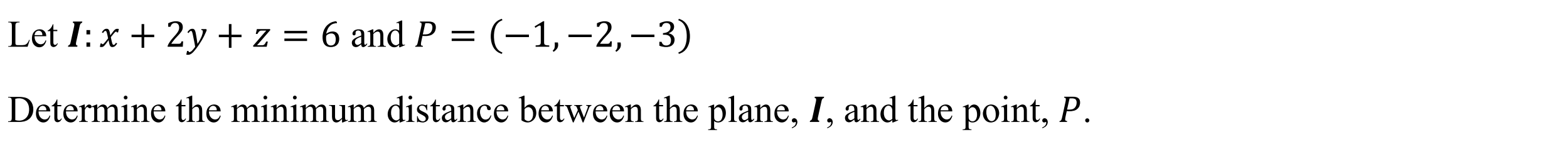

Intersection between 2 lines (ints2l)
Function: Determines the point of intersection & angle between two lines
Syntax: ints2l(Line Vector 1, Line Vector 2)
Example:
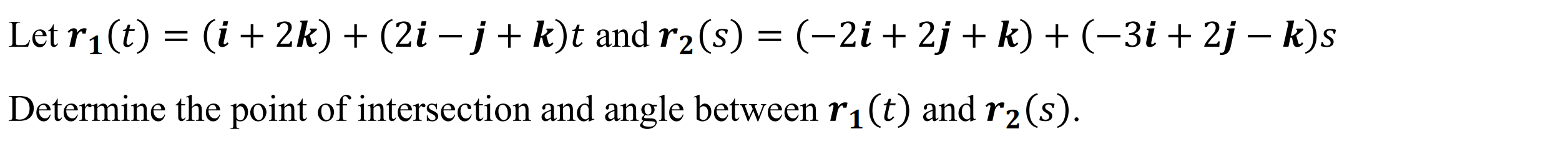

Intersection between 2 planes (ints2pl)
Function: Determines the line of intersection & angle between two planes
Syntax: ints2pl(Plane Cartesian 1, Plane Cartesian 2)
Example:
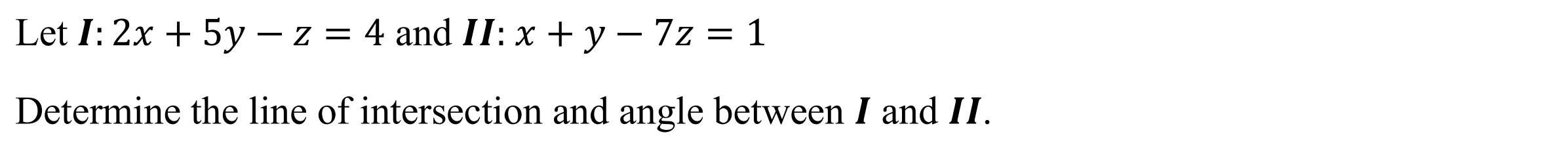

Intersection between plane and line (intslpl)
Function: Determines the point of intersection & angle between line and plane
Syntax: intslpl(Line Vector, Plane Cartesian)
Example:
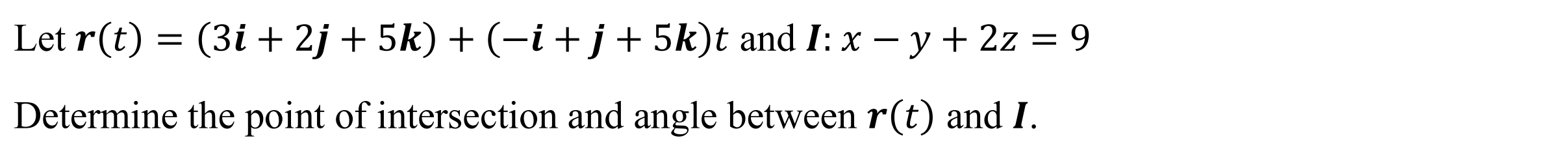

Create line with 2 points (line2p)
Function: Determines the equation of a line given two points
Syntax: line2p(Point 1, Point 2)
Example:
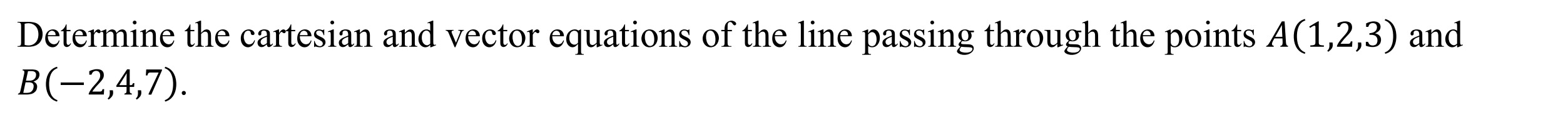

Create line with direction vector and point (linedp)
Function: Determines the equation of a line given a direction vector and point
Syntax: linedp(Direction Vector, Point)
Example:


Create plane with 3 points (plane3p)
Function: Determines the equation of a plane given three points
Syntax: plane3p(Point 1, Point 2, Point 3)
Example:


Create plane with normal and point (planenp)
Function: Determines the equation of a plane given a normal vector and a point
Syntax: planenp(Normal Vector, Point)
Example:


Plane formed by intersecting lines (planeintl)
Function: Determines the equation of the plane formed by two intersecting lines
Syntax: planeintl(Line Vector 1, Line Vector 2)
Example:
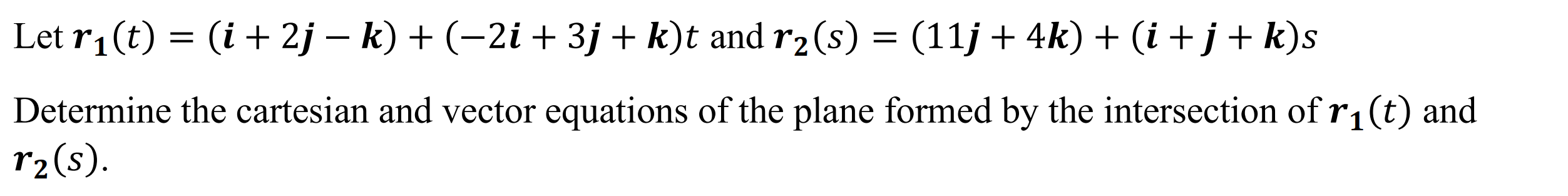

Probability
Sample Mean Confidence Interval (confint)
Function: Determines the confidence interval for the sample mean
Syntax: confint(Sample Mean, Population Standard Deviation, Sample Size, . confidence)
Example:
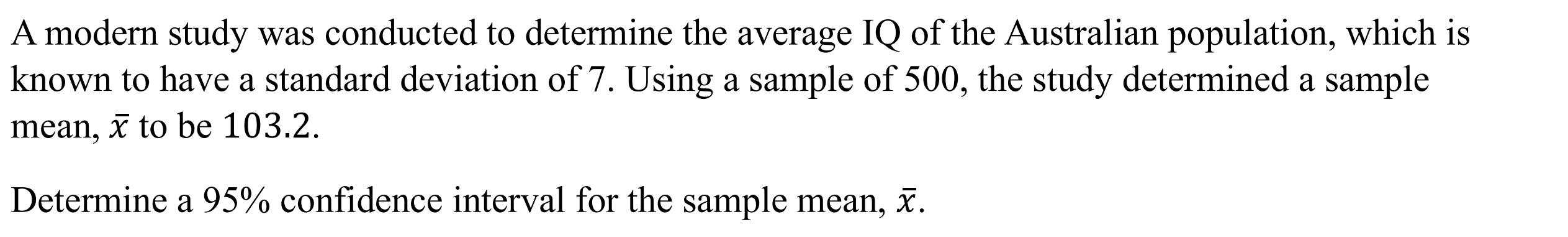

Hypothesis Testing (hyptest)
Function: Determines whether the null hypothesis should be rejected by calculating p-values
Syntax: hyptest() (You will be prompted for inputs)
Example:


Probability of Error (prerror)
Function: Determines the probability of Type I and Type II errors occuring
Syntax: prerror() (You will be prompted for inputs)
Example:


p-value (pval)
Function: Determines the p-value of a hypothesis test
Syntax: pval() (You will be prompted for inputs)
Example:

