Mathematical Methods UDFs
Calculus
Average Rate of Change (avgroc)
Function: Determines the average rate of change of a function
Syntax: avgroc(function, variable, lower, upper)
Example:
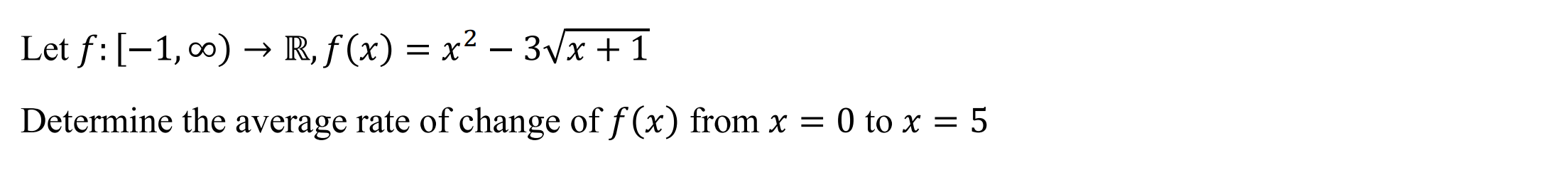

Average Value (avgval)
Function: Calculates the average value of a function
Syntax: avgval(function, variable, lower, upper)
Example:
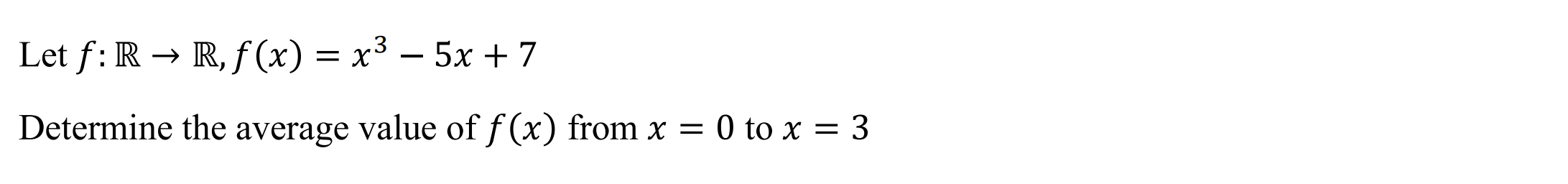

Bound Area (boundarea)
Function: Determines the area bound by two graphs (if any) across their maximal domains
Syntax: boundarea(function1, function2, variable)
Example:
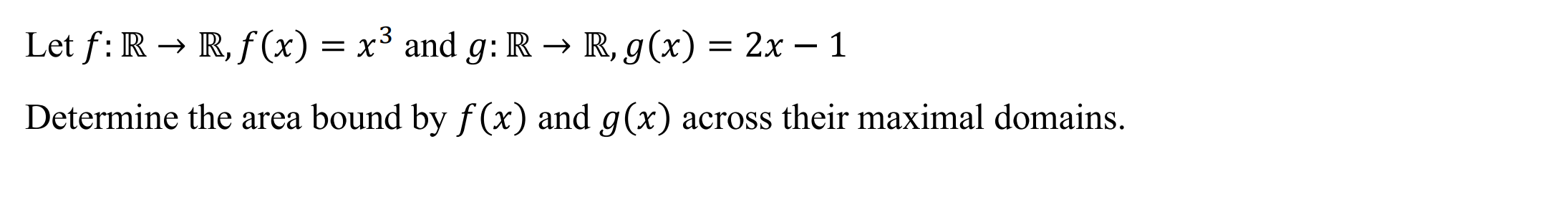

Bound Area with domain (boundaread)
Function: Determines the bound area between two functions in a restricted domain
Syntax: boundaread(function1, function2, variable, lower, upper)
Example:
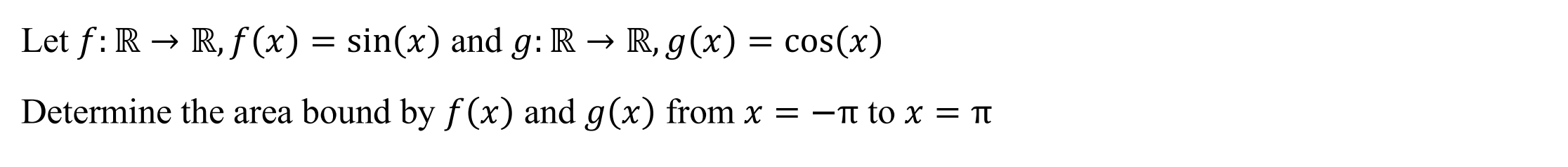

Integral Solve (intsolve)
Function: Determines the answer for the integration multiple choice questions
Case 1: One integral given, find transformed integral
Syntax: intsolve({lower1,upper1, value1}, {transformations}, {lower2, upper2})
Example:
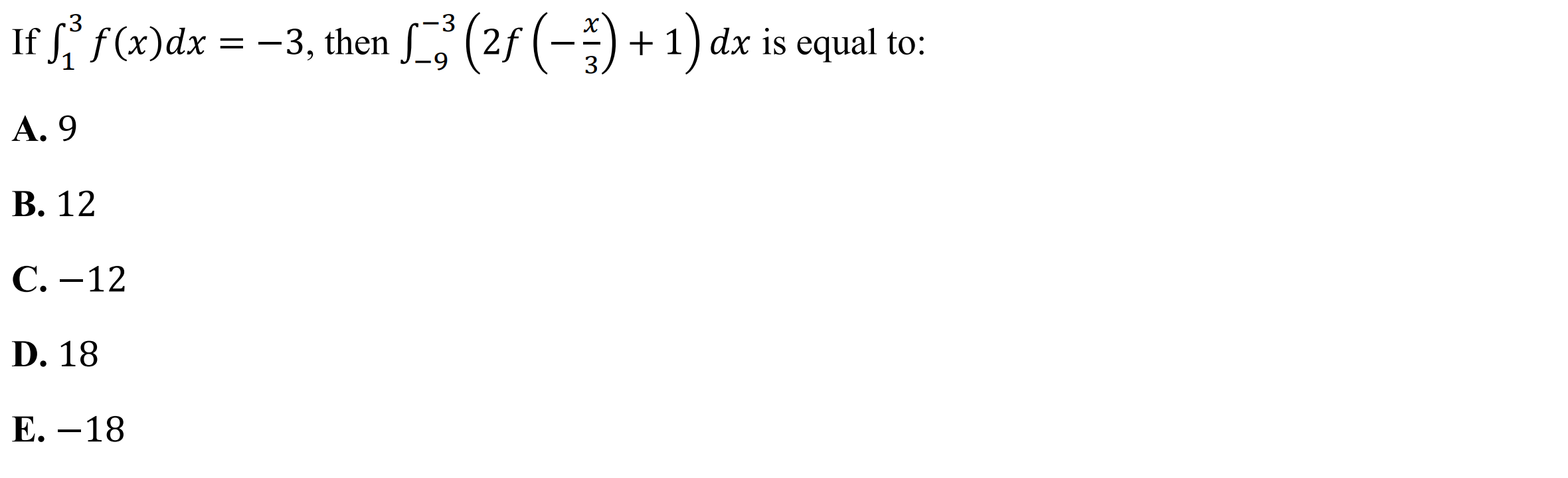

Case 2: Two integrals given, find untransformed integral
Syntax: intsolve({lower1, upper1, value1}, {lower2, upper2, value2}, {lower3, upper3})
Example:
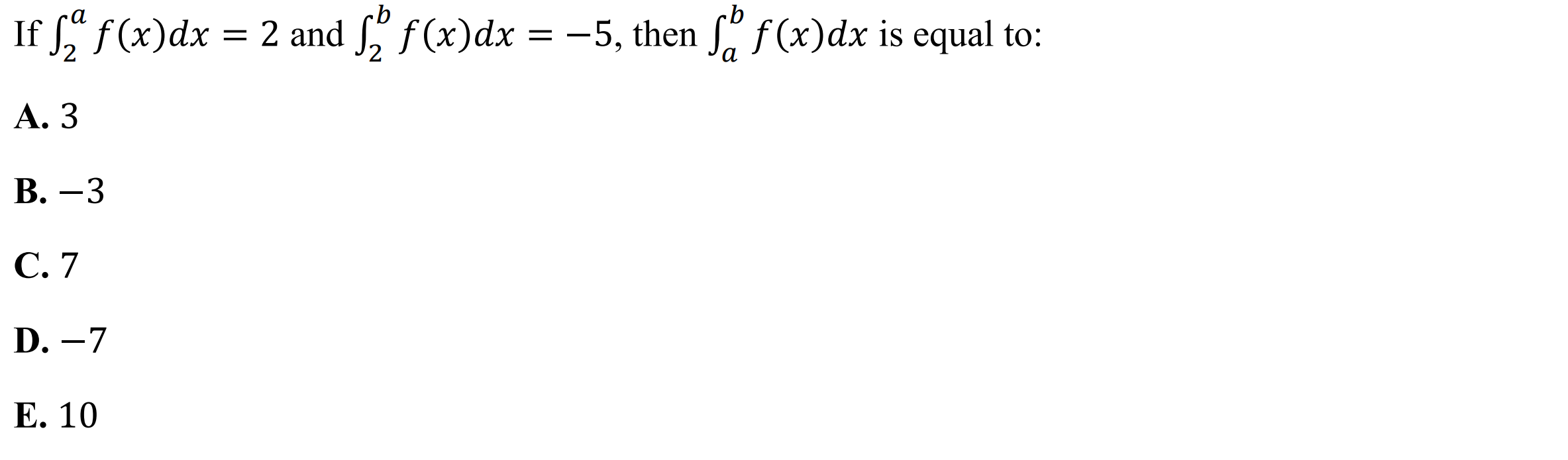

Case 3: Two integrals given, find transformed integral
Syntax: intsolve({lower1, upper1, value1, lower2, upper2, value2}, {transformations}, {lower3, upper3})
Example:
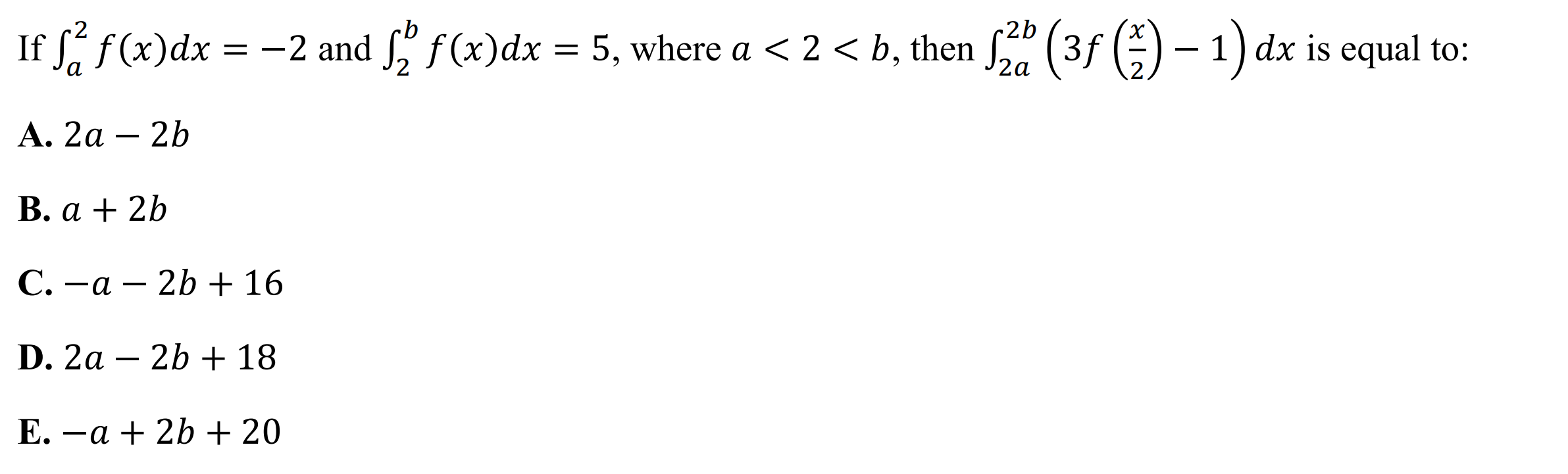

Newton's Method (newtons)
Function: Estimates the root of a function using newton's method
Syntax: newtons(function, variable, x0, iterations)
Example:


Number of Roots (nroot)
Function: Determines the value(s) of a parameter required for a specified number of roots.
Syntax: nroot(polynomial, variable, parameter, number of roots)
Example:
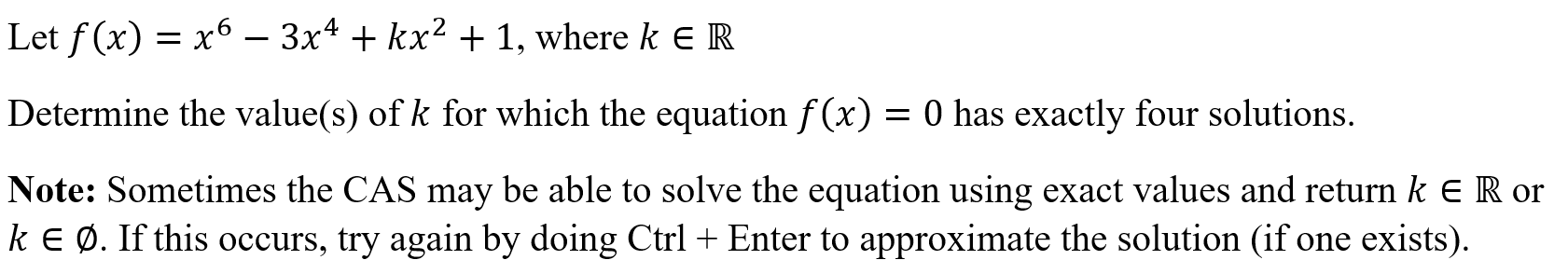

Number of Stationary Points (nstp)
Function: Determines the value(s) of a parameter required for a specified number of stationary points.
Syntax: nstp(polynomial, variable, parameter, number of stationary points)
Example:


Number of Points of Inflection (npoi)
Function: Determines the value(s) of a parameter required for a specified number of points of inflection.
Syntax: npoi(polynomial, variable, parameter, number of points of inflection)
Example:


Points of Inflection (pois)
Function: Determines the points of inflection of a function
Syntax: pois(function, variable)
Example:


Sign Table (signtab)
Function: Uses a sign table to determine the stationary points of a function and their nature
Syntax: signtab(function, variable)
Example:


Stationary Points (stps)
Function: Determines the stationary points of a function
Syntax: stps(function, variable)
Example:


Tangent Solve (tangsolve)
Function: Determines the equation of the tangents to a function which pass through a specified point
Syntax: tangsolve(function, variable, x-coordinate, y-coordinate)
Example:
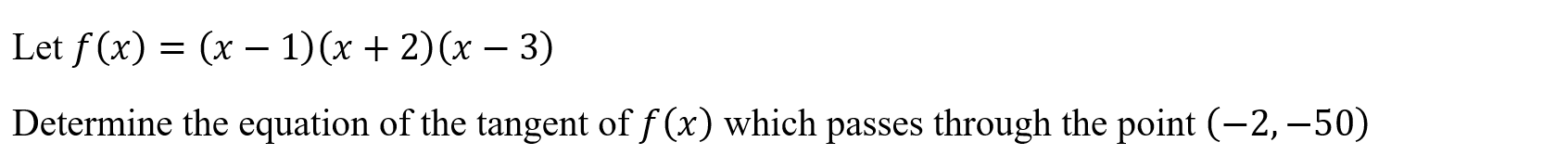

Trapezoid Approximation (trapapprox)
Function: Approximates an integral using the trapezoidal rule
Syntax: trapapprox(function, variable, lower, upper, number of trapezia)
Example:
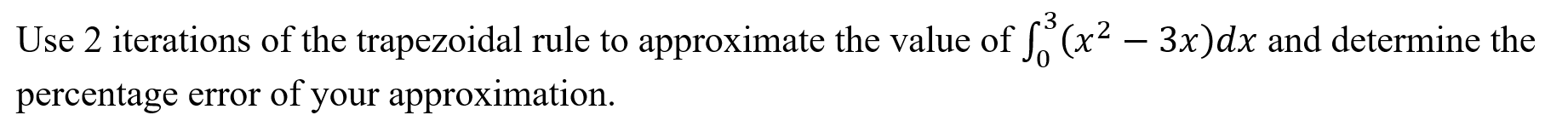

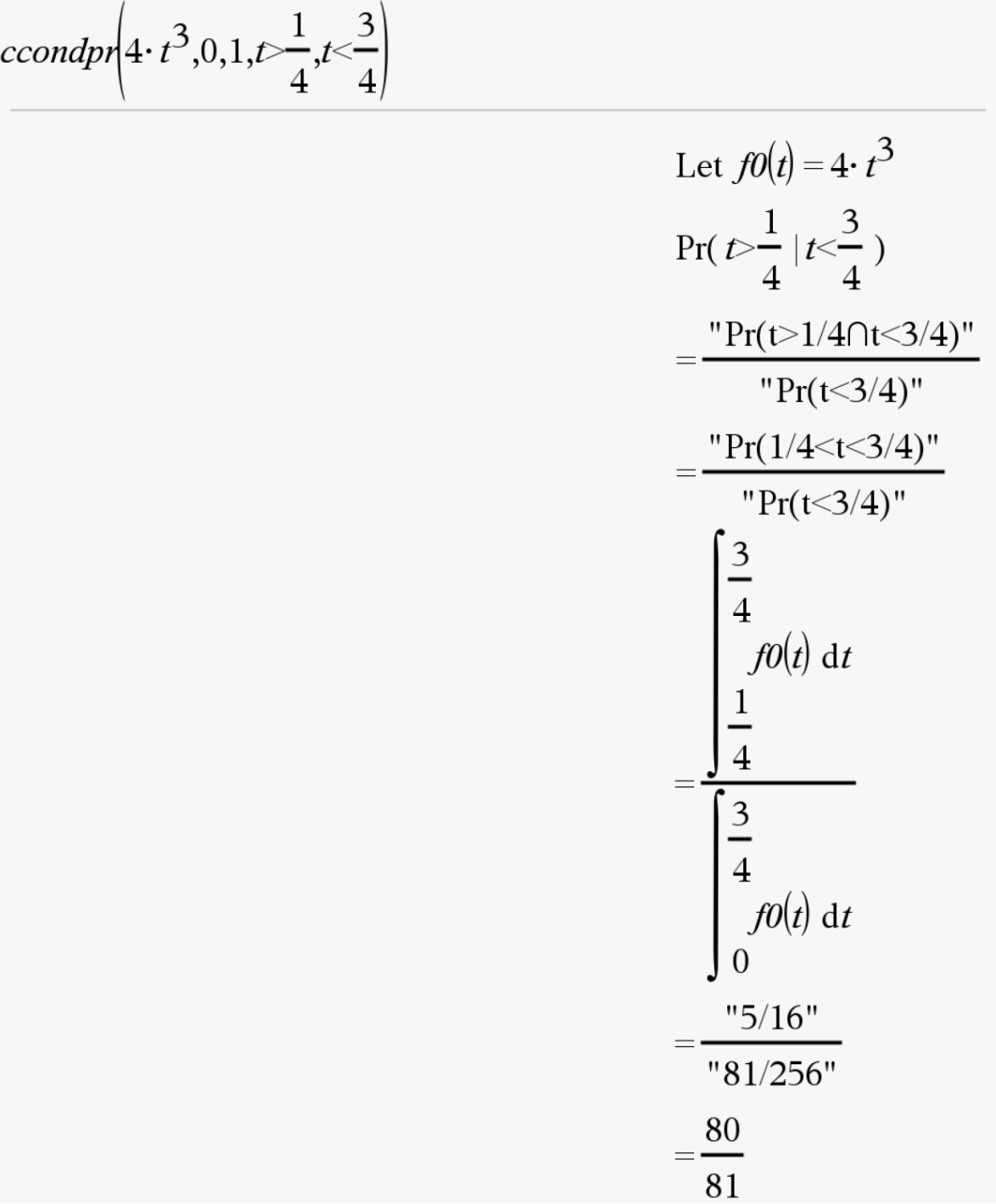
Continuous Probability
Continuous Conditional Probability (ccondpr)
Function: Determines conditional probability for a continuous distribution
Case 1: Probability density function
Syntax: ccondpr(Probability Density Function, Lower Bound, Upper Bound, Condition 1, Condition 2)
Example:
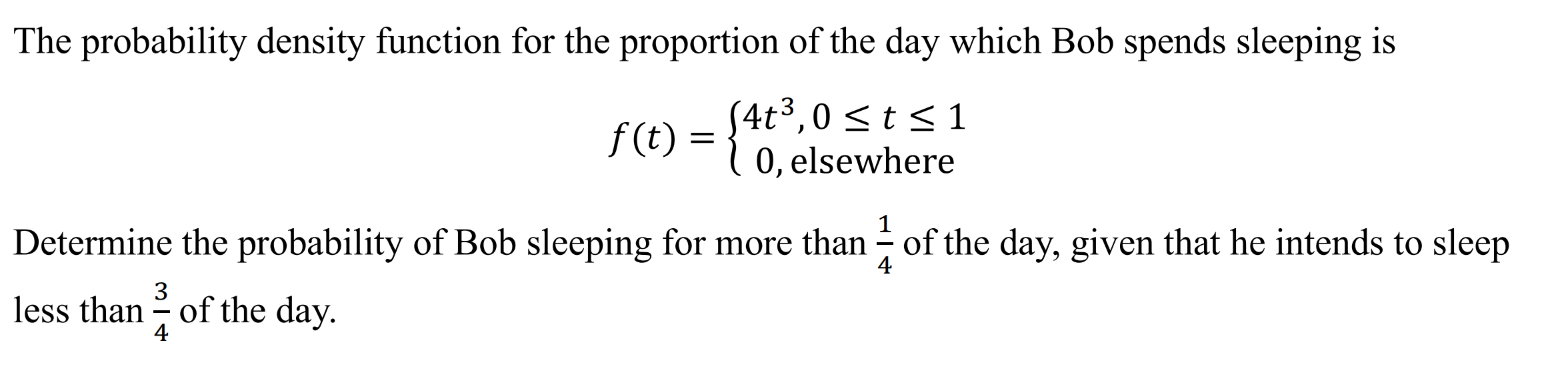
Case 2: Normal Distribution
Syntax: ccondpr(Blank String, Mean, Standard Deviation, Condition 1, Condition 2)
Example:


Confidence Interval (confint)
Function: Determines a confidence interval as well as the z-score, margin of error and standard deviation
Syntax: confint(Sample Size,P_hat, . confidence)
Example:


Confidence Interval Solve (confintsolve)
Function: Determines the sample size, standard deviation or percentage confidence depending on the provided data
Syntax: confintsolve(Lower Bound, Upper Bound, Sample Size or Sample Standard Deviation or . Confidence)
Example:


Continuous Distribution Information (continfo)
Function: Determines the expected value, mean, variance, standard deviation of a continuous probability distribution
Syntax: continfo(function, variable, lower, upper)
Example:


Inverse Normal (invnormvals)
Function: Determines the left, right and centre possibilities for probability of a distribution
Syntax: invnormvals(mean, standard deviation, probability)
Example:
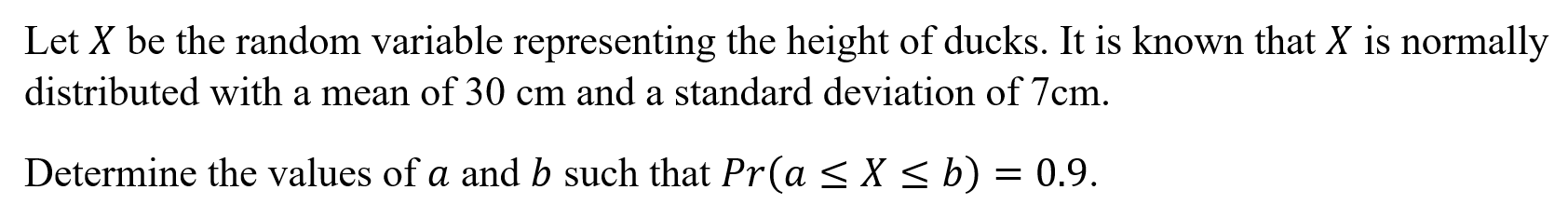

Normal Solve (normsolve)
Function: Determines the mean and standard deviation for lower and upper type questions
Case 1: Both Lower and Upper given
Syntax: normsolve(Lower, Probability of Lower, Upper, Probability of Upper)
Example:


Case 2: Lower and Mean given
Syntax: normsolve(Lower, Probability of Lower, Mean, Blank String)
Example:


Case 3: Lower and Standard Deviation given
Syntax: normsolve(Lower, Probability of Lower, Blank String, Standard Deviation)
Example:


Case 4: Upper and Mean given
Syntax: normsolve(Mean, Blank String, Upper, Probability of Upper)
Example:


Case 5: Upper and Standard Deviation given
Syntax: normsolve(Blank String, Standard Deviation, Upper, Probability of Upper)
Example:


Discrete Probability
Binomial Distribution Information (binominfo)
Function: Determines the expected value, variance, standard deviation, sample expected value, and sample standard deviation for a binomial distribution
Syntax: binominfo(Sample Size, Probability of Success)
Example:


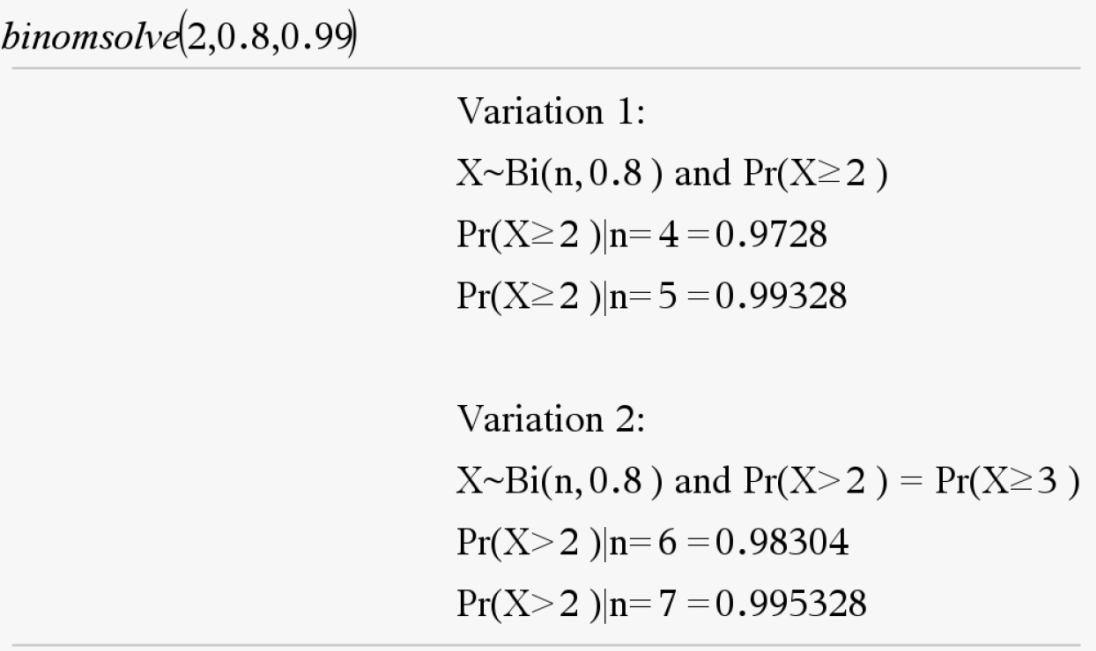
Binomial Solve (binomsolve)
Function: Determines the number of trials required to achieve a certain probability
Syntax: binomsolve(outcome, probability of success, threshold value)
Example:

Discrete Conditional Probability (dcondpr)
Function: Determines conditional probability for a discrete distribution
Case 1: Binomial Distribution
Syntax: dcondpr(number of trials, probability of success, condition 1, condition 2)
Example:


Case 2: Discrete Probability Table
Syntax: dcondpr({List containing outcomes}, {List containing probabilities}, condition 1, condition 2)
Example:


Case 3: Probability Mass Function
Syntax: dcondpr({List containing outcomes}, PMF, condition 1, condition 2)
Example:


Hypergeometric Cumulative Probability Function (hypergeocdf)
Function: Determines the probability of selecting items without replacement, but over an interval of outcomes
Syntax: hypergeocdf(sample size, population size, number of successful items, lower bound, upper bound)
Example:


Hypergeometric Probability Density Function (hypergeopdf)
Function: Determines the probability of selecting items without replacement, but for specific outcomes
Syntax: hypergeopdf(sample size, population size, number of successful items, outcome)
Example:


Inverse Binomial (invbinomial)
Function: Determines the outcome required to achieve the probability
Syntax: invbinomial(number of trials, probability of success, known probability value)
Example:


Probability Table (prtable)
Function: Determines the mean, variance, standard deviation of a probability table
Syntax: prtable({outcomes}, {probabilities})
Example:


Sample Distribution Binomial (samplebinom)
Function: Determines the distribution for the sample proportion of a binomially distributed sample
Syntax: samplebinom(Sample Size, Probability of Success)
Example:


Sample Binomial Probability (samplebinompr)
Function: Determines the probability for the sample proportion for a binomially distributed sample
Syntax: samplebinompr(Sample Size, Probability of Success, Lower, Upper)
Example:
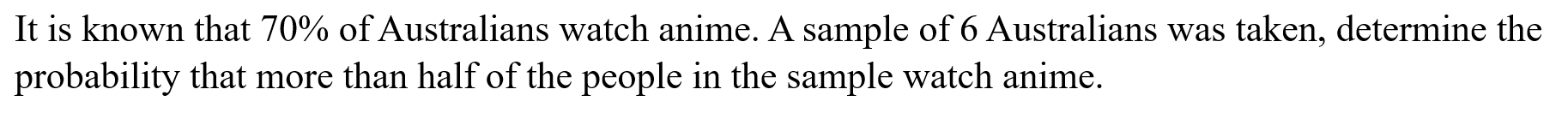

Sample Distribution Hypergeometric (samplehypergeo)
Function: Determines the distribution for the sample proportion of a hypergeometrically distributed sample
Syntax: samplehypergeo(Sample Size, Population Size, Number Successful)
Example:


Sample Hypergeometric probability (samplehyppr)
Function: Determines the probability for the sample proportion for a hypergeometrically distributed sample
Syntax: samplehyppr(Sample Size, Population Size, Number Successful, Lower, Upper)
Example:


Functions
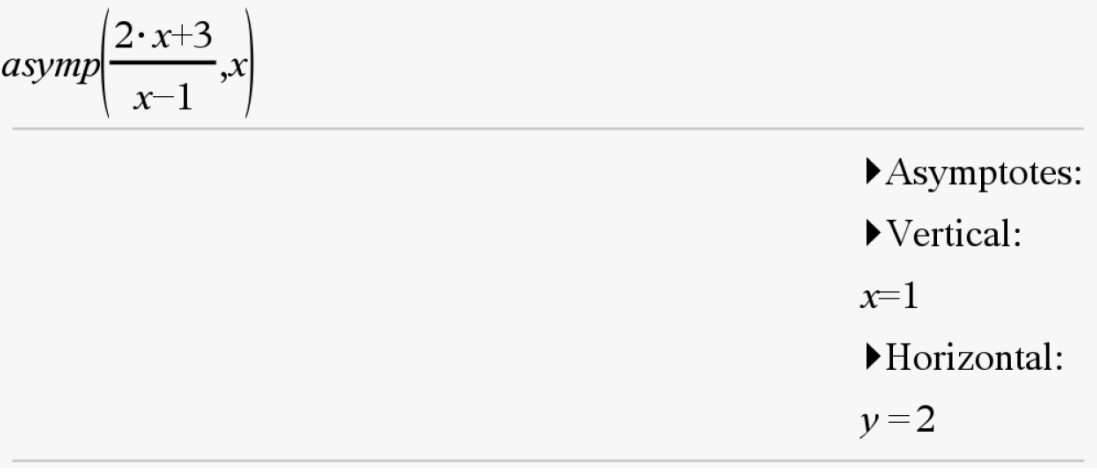
Asymptotes (asymp)
Function: Determines the vertical and horizontal asymptotes of a function
Syntax: asymp(function, variable)
Example:

Composite Check (ccheck)
Function: Checks whether a composite function is valid, and the maximal domain required for the composite to be valid.
Syntax: ccheck(function 1, function 2)
Example:
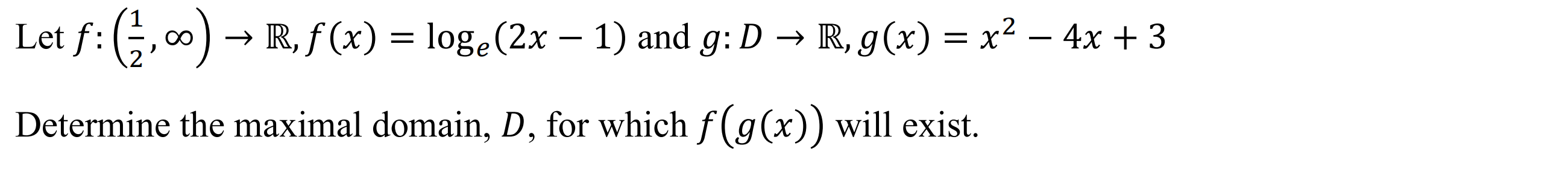

Discriminant (discrim)
Function: Calculates the discriminant of an inputted quadratic expression
Syntax: discrim(quadratic Expr, variable)
Example:
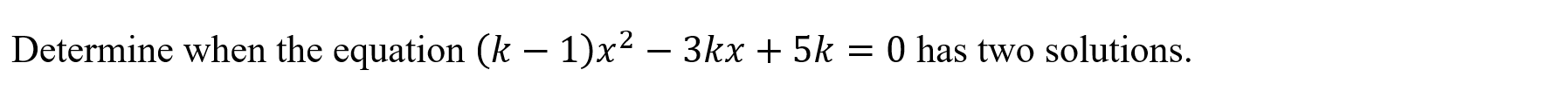

Domain and Range (domrang)
Function: Determines the domain and range of a function
Syntax: domrang(function, variable)
Example:


Intercepts (intercepts)
Function: Finding the x and y intercepts of a function
Syntax: intercepts(function,variable)
Example:
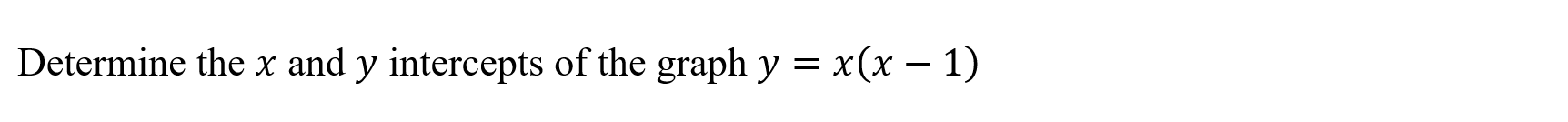

Intersects (intersects)
Function: Determines the points of intersection of two functions across their maximal domains.
Syntax: intersects(function1,function2,variable)
Example:
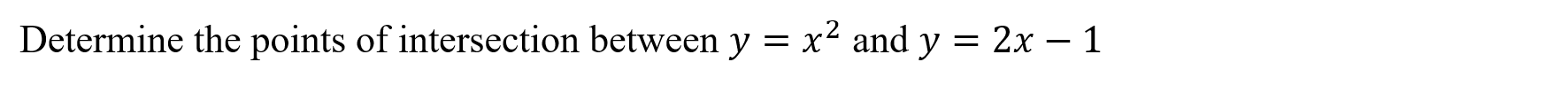

Intersects with domain (intersectsd)
Function: Determines the points of intersection between two functions in a restricted domain
Syntax: intersectsd(function1, function2, variable, lower, upper)
Example:
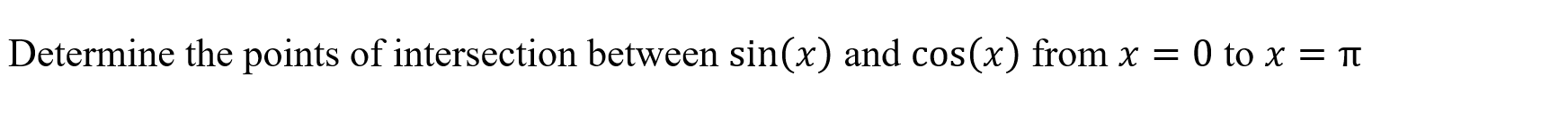

Inverse Function (inverse)
Function: Determines the inverse of a function
Syntax: inverse(function, variable, x in domain of f)
Example:


Inverse Intersections (invints)
Function: Determines the values of a parameter, k, required for a function and its inverse function to have a certain number of intersections
Case 1: Square Root
Syntax: invints(function, number of intersections with inverse)
Example:
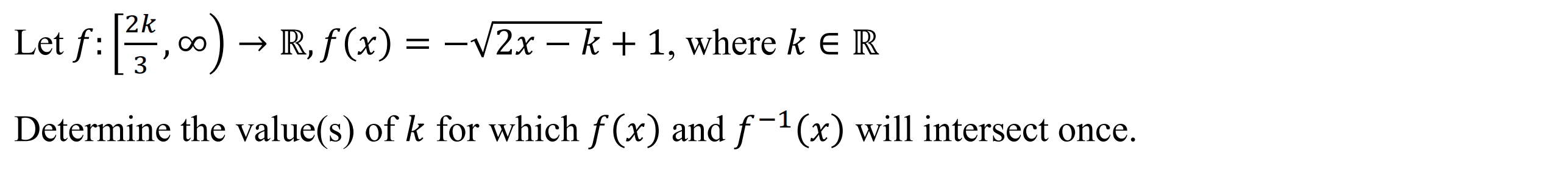

Case 2: Parabola
Syntax: invints(function, number of intersections with inverse) *You will be prompted to enter an initial condition
Example:
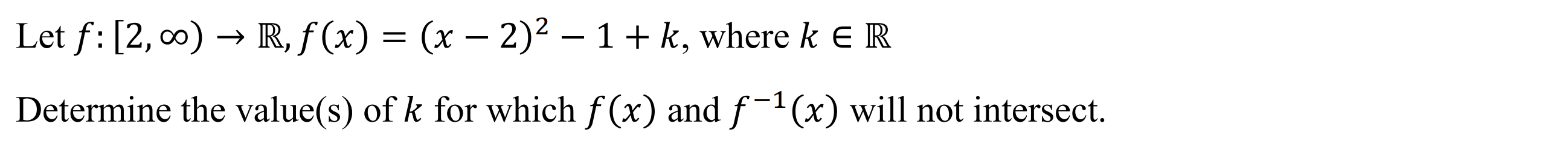

Case 3: Exponential
Syntax: invints(function, number of intersections with inverse)
Example:
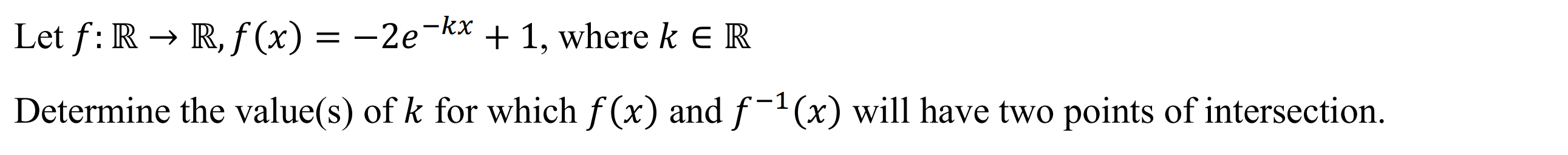

Case 4: Logarithm
Syntax: invints(function, number of intersections with inverse)
Example:
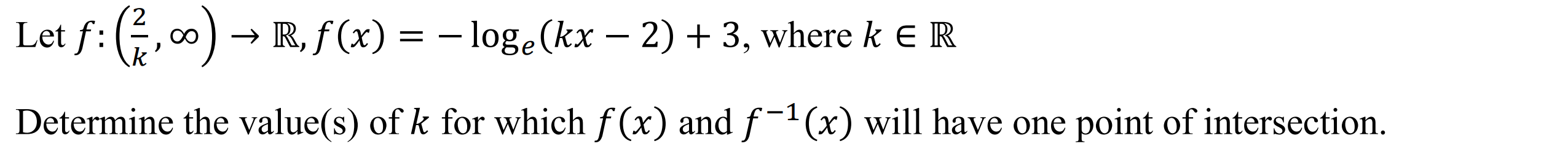

Case 5: Hyperbola
Syntax: invints(function, number of intersections with inverse)
Example:
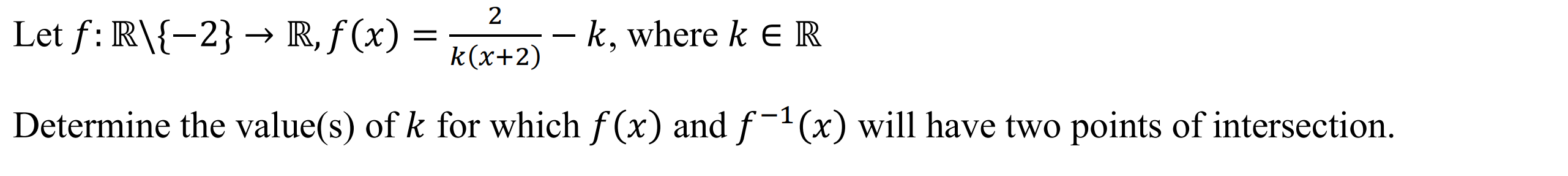

Case 6: Simple Cubic (Either 0 or 1 turning points)
Syntax: invints(function, number of intersections with inverse)
Example:
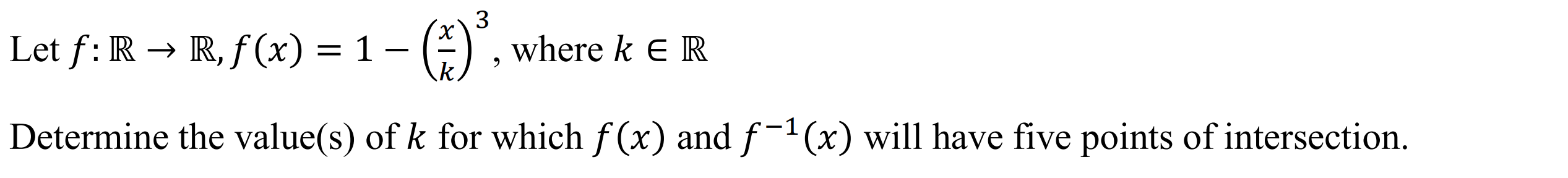
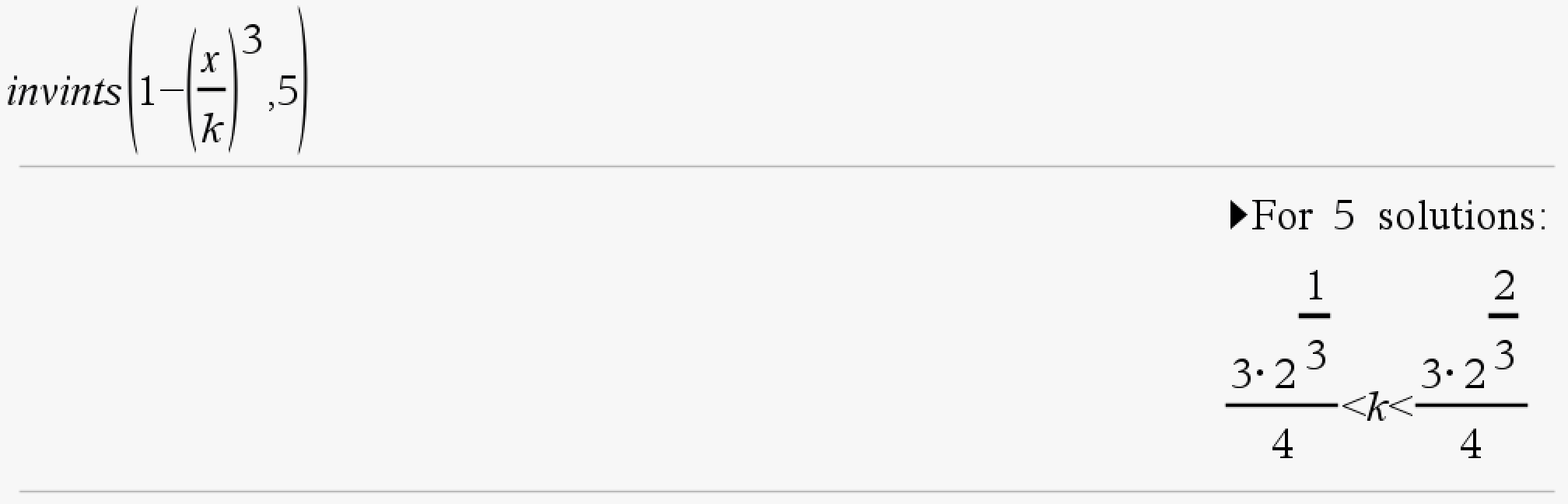
Case 7: Complicated Cubic (More than 1 turning point)
Syntax: invints(function, number of intersections with inverse) *You will be prompted to enter the domain
Example:
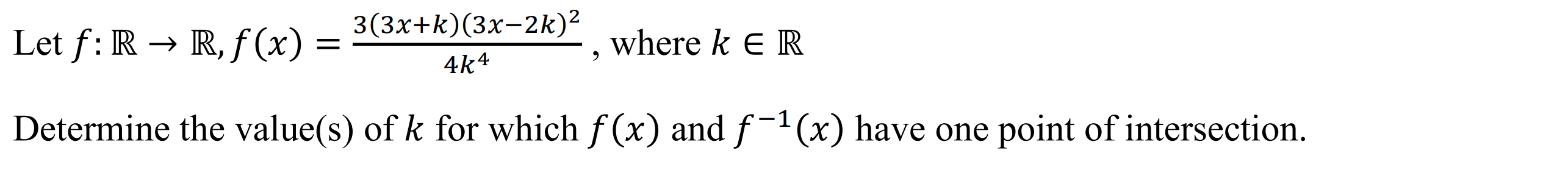
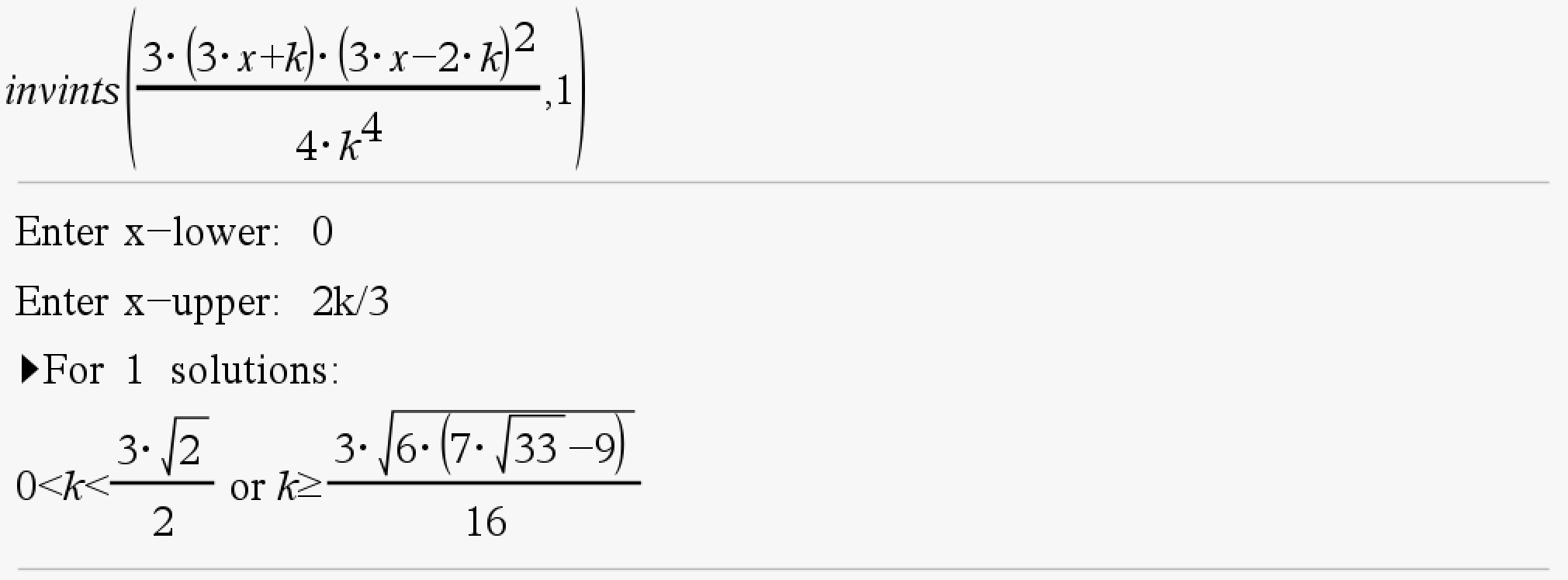
Angle Between Two Lines (lineang)
Function: Determines the angle between two lines in degrees (Assumes CAS in raidans mode)
Syntax: lineang(Line 1, Line 2, Variable)
Example:
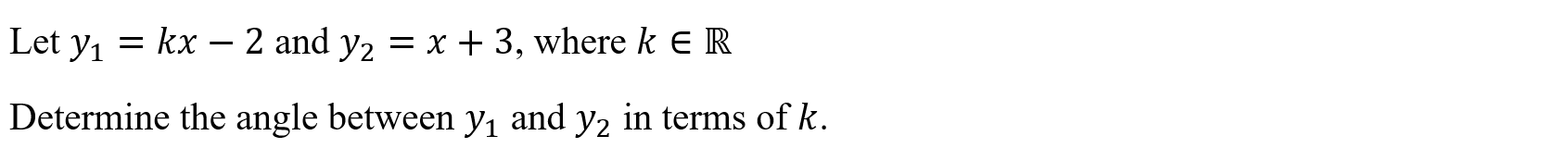

Unique, None, Infinite Solution (linesolve)
Function: Determines when two linear equations will have an unique, none or infinitely many solutions. Note: Equations must be in the form: Ax + By = C , rather than Ax + By + C = 0
Syntax: linesolve(Equation1, Equation2)
Example:
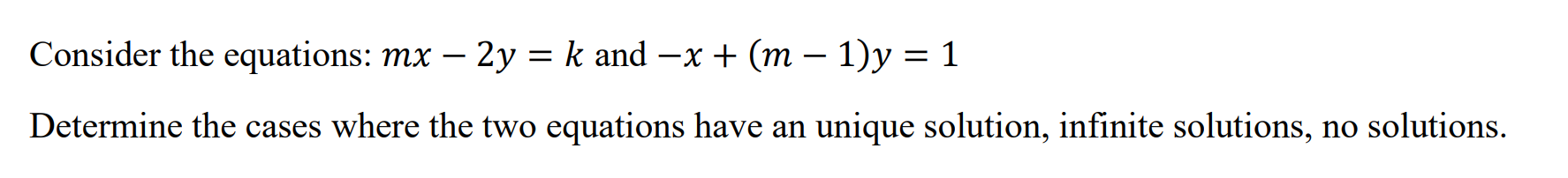

Property Check (pcheck)
Function: Determines which function satisfies a specific property
Syntax: pcheck(function, variable, LHS, RHS)
Example:
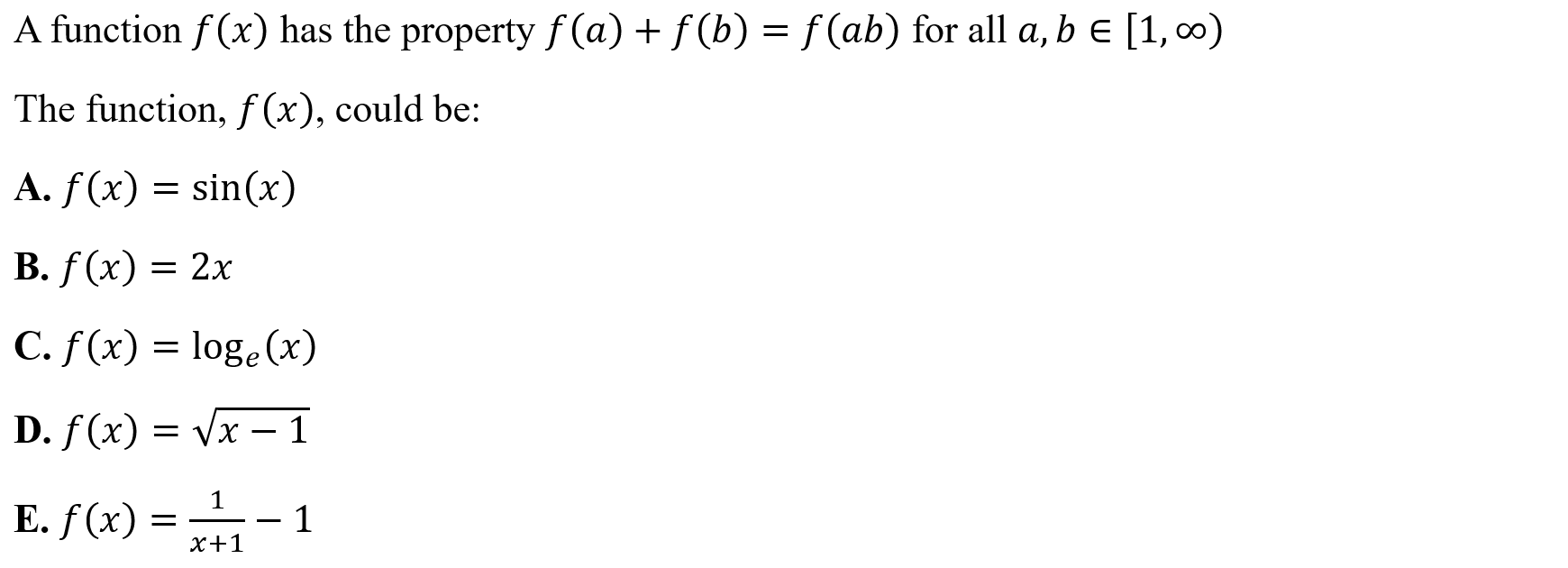
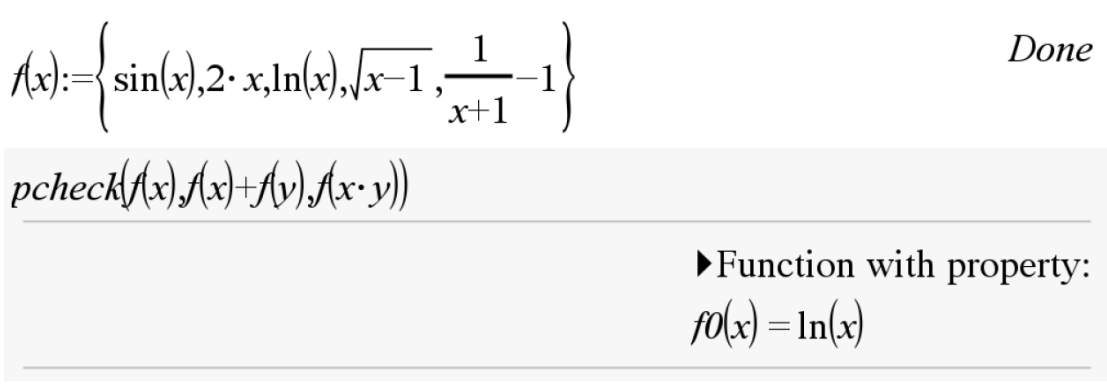
Point Information (pointinfo)
Function: Determines the gradient, perpendicular gradient, line, x and y intercepts of a line, midpoint, distance
Syntax: pointinfo(x1, y1, x2, y2)
Example:
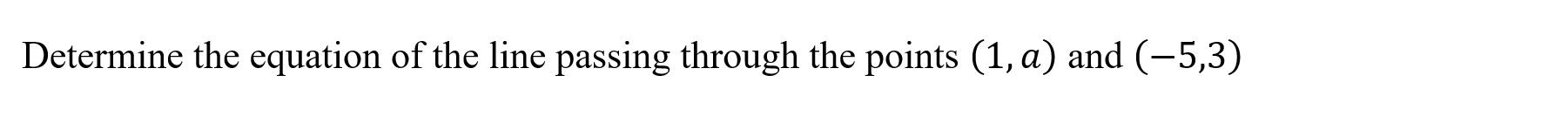

Polynomial Fit (polyfit)
Function: Determines the equation of a polynomial which passes through a set of points.
Syntax: polyfit({x1, y1, x2, y2, ...})
Example:
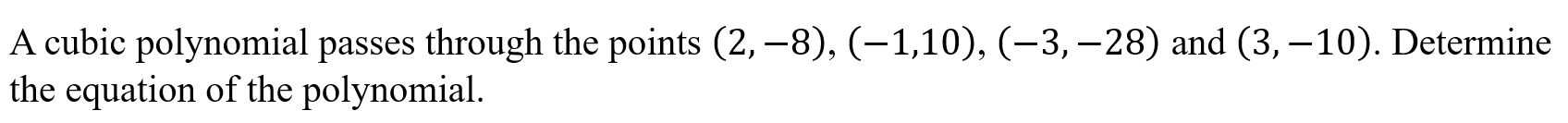

Transformations (transform)
Function: Determines the transformed function after applying certain transformations
Syntax: transform(function, {transformations})
Example:


Miscellaneous
Column Augment (ca)
Function: Converts answer into easily readable matrix form
Case 1: One Variable
Syntax: surfarea(Function, t, Lower Bound, Upper Bound)
Example:


Case 2: Multiple Variables (Up to 5)
Syntax: ca(Ans, {var1, var2,..., var5}
Example:

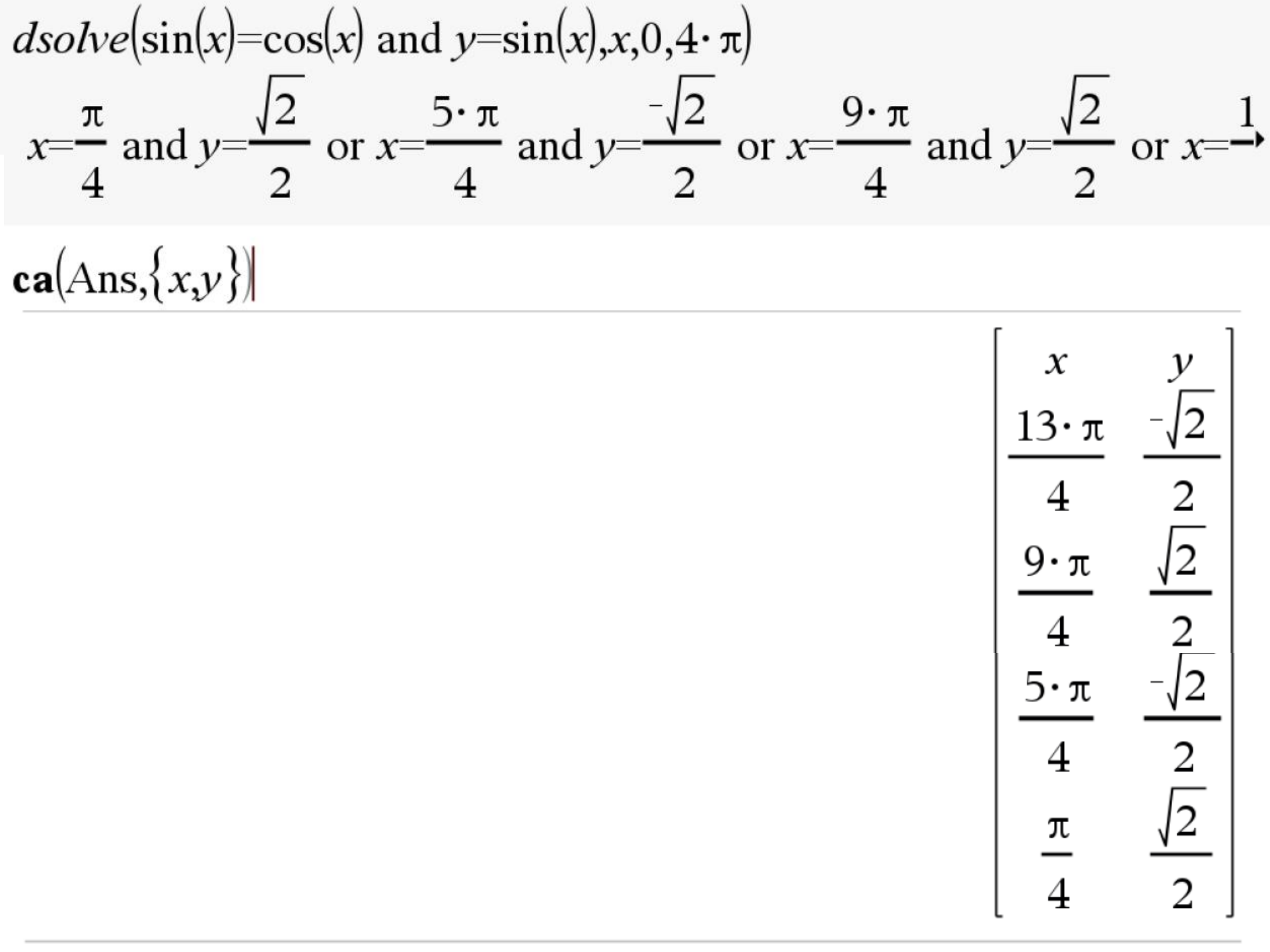
Domain Solve (dsolve)
Function: Solves equations in a restricted domain
Syntax: dsolve(Equation, Variable, Lower Bound, Upper Bound)
Example:
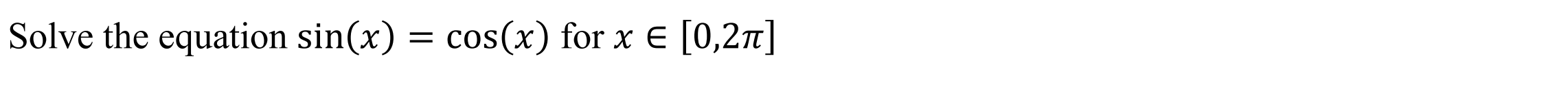

Graph Information (graphinfo)
Function: Determines the endpoints, x-intercepts, y-intercepts, stationary points, points of inflection of a function
Case 1: Restricted Domain
Syntax: graphinfo(Function, Variable, Lower Bound, Upper Bound)
Example:
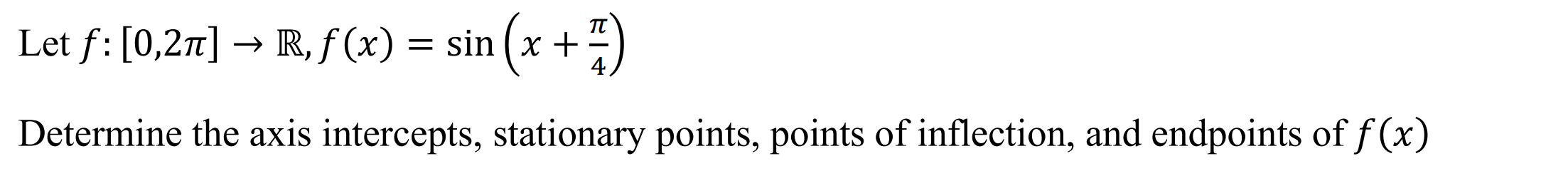

Case 2: Across Maximal Domain
Syntax: graphinfo(Function, Variable, Blank String, Random Character)
Example:


Rewrite (rr)
Function: Gets the right hand side of an equation/answer
Syntax: rr(Equation/Answer)
Example:

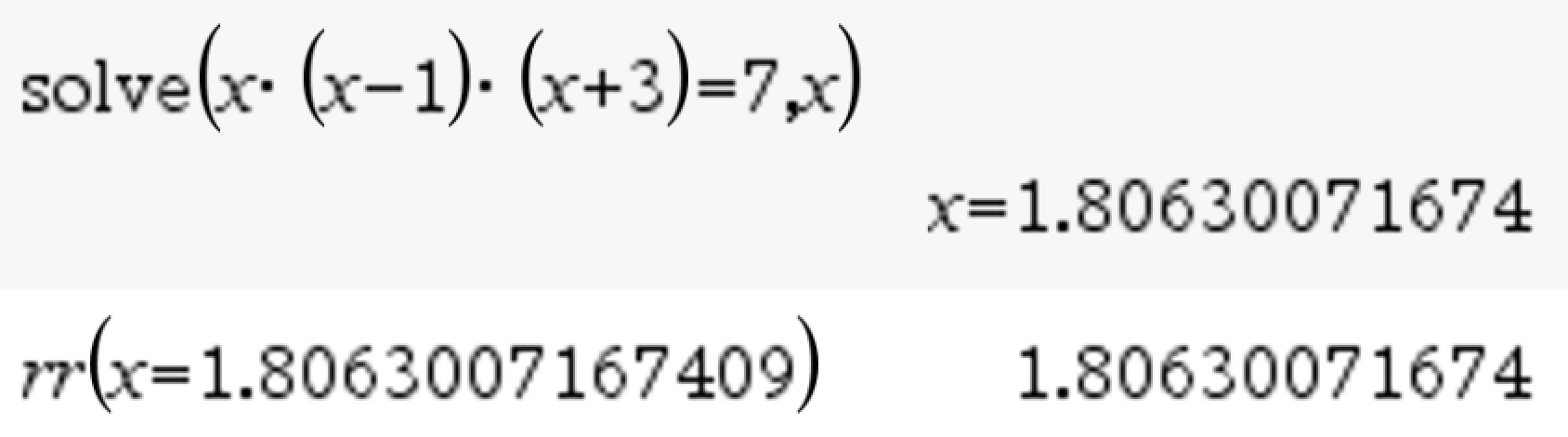
Triganometric Solve (tsolve)
Function: Gives exact values of circular function equations (Ones which TiNspire cannot properly solve on its own)
Case 1: Trigonometric Equation
Syntax: tsolve(Equation, Variable, Lower Bound, Upper Bound)
Example:


Case 2: Trigonometric Inequality
Syntax: tsolve(Inequality, Variable, Lower Bound, Upper Bound)
Example:

